Der Ovaldreher  sollte von  Ellipsen zumindest  das Folgende  aus seinen Schulbüchern wissen.

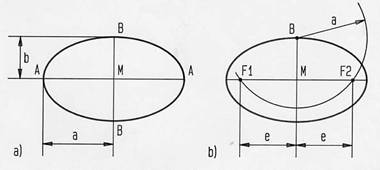
                            Bild2101 Ellipsenachsen und lineare Exzentrizität
                                                           a)  Halbachsen
                                                           b) Brennpunkte

Die Ellipse ist ein Kegelschnitt; man erhält sie, wenn man  einen Kreiskegel oder einen Kreiszylinder schräg  durchschneidet.   Sie hat zwei Achsen,  die im  Mittelpunkt M  der Ellipse  aufeinander senkrecht stehen (Bild 2101a). Die Halbachsen haben die Länge AM = a und BM = b. Die Halbachsen sind die beiden  wichtigen Maße  für das Ovaldrehen. Meistens sind sie gegeben.

Einzustellen ist am Ovalwerk die

     Halbachsen-Differenz    d = a - b,

sie ist nicht zu verwechseln mit dem

     Achsenverhältnis              ß  = b/a

abgekürzt  mit  dem  Buchstaben  ß  (beta), das für die Einstellung des Indexers eine Rolle spielt. Ein anderes Maß ist die

      lineare Exzentrizität        e .

Sie wird nicht für die Einstellung am Ovalwerk benötigt, ist aber nötig für das Aufzeichnen der Ellipse  mit der  Fadenkonstruktion (Gärtnerkonstruktion). Die lineare Exzentrizität ist der halbe Abstand der beiden Brennpunkte F1  und F2  der Ellipse  auf ihrer großen Achse, der Hauptachse. Man erhält sie durch einen Kreisbogen um B mit dem Radius a (Bild 2101b ) oder mit der Formel

                                             e  = √ (a² − b²).

Von Bedeutung ist noch der  Ellipsen-Umfang u, der nicht  exakt, sondern nur durch eine Näherungsformel berechnet werden kann: 

                                           u ≈ π(1,5(a + b) - √ab )                 oder mit ß = b/a 

                                          u ≈ aπ(1,5(1 + ß)-√ß).

Der Flächeninhalt A einer Ellipse ist              A = abπ

Am  einfachsten ist das Aufzeichnen einer Ellipse mit der Fadenkonstruktion, z. B. für das  Zuschneiden eines elliptischen Rohlings aus einem Brett oder Block. Dazu zeichnet man die beiden Achsen AA und BB in der gewünschten Länge mit  ihrem Schnittpunkt M auf das Brett, nimmt die große Halbachse MA = a  in den  Zirkel und schlägt - wie in Bild 2101b  - um  einen der  Endpunkte B  der kleinen Achse einen Kreisbogen. Er schneidet die  große Achse  in den beiden Brennpunkten F1 und F2. In diese und in B schlägt man je einen Nagel und legt um diese 3 Nägel eine Fadenschlinge (Bild 2102a). Der  Nagel in  B wird  herausgezogen und  die Ellipse  mit einem Stift bei straffem Faden gezeichnet (Bild 2102b).

 Fadenkonstruktion der Ellipse

  
 
 
 
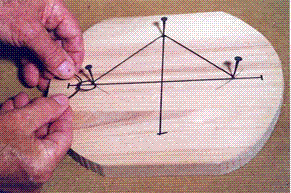
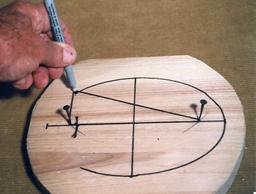
Bild 2102a  Fadenschlinge um 3 Nägel                    Bild 2102b  Zeichnen der Ellipse                                                                    

Ellipsenzirkel (Ellipsographen) sind  Mechanismen, die einen Stift auf einer  Ellipse auf  dem festliegenden Zeichenblatt führen. Statt des Zeichenstiftes  kann ein  Glasschneider  oder  ein  Messer  zum  Schneiden von  Karton  eingesetzt  werden. Die  Ellipsenachsen  können am  Ellipsenzirkel  eingestellt werden.  Das kinematische Prinzip der  Ellipsenzirkel ist zumeist der Doppelschieber (englisch: trammel) [6.5], Bild 2103.  In einem feststehenden Kreuzschlitz 3 laufen die Schieber 2 und 4. Sie sind in ihren Gelenken A und B durch eine Koppel 1 verbunden, deren Punkt C die Ellipse k_C  in die feststehende Ebene schreibt. Die  Einstellung  der  gewünschten Halbachsen  erfolgt durch  die Abstände BC = a und AC = b. Der Abstand AB = a - b =  d ist  die Halbachsen-Differenz. Der Mittelpunkt M der Strecke AB läuft auf einem Kreis k_M um den Ellipsen-Mittelpunkt M₀. Der Radius ist r  = d/2.

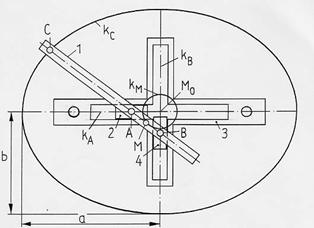
Bild 2103 Kinematisches Schema des  
Ellipsenzirkels (Doppelschieber, trammel) [6.5]

Mit den Ellipsenzirkeln in  den folgenden  beiden Bildern  können Ellipsen  gezeichnet  und  aus  Papier  und  Karton  mit  Messern geschnitten  werden.  Für Glas  ist  ein Glasschneider  (Hartmetallrad) einsetzbar.  

Bild 2104
Ellipsen- und Kreis-Glasschneider
(Firma  J. Bohle, D 42755 Hann)

  Bild 2105 Ellipsenzeichengerät (Ellipsograph)
  (Gebrüder Haff GmbH,  D 87459 Pfronten)

Der  Ellipsenzirkel  in  Bild  2106  zeichnet  bzw. schneidet  die Ellipse neben sich. Das  erlaubt kleinste  Ellipsen zu  erzeugen. Der Mechanismus entspricht einem Patent von F. O. Kopp. Für seine Einstellung für gegebene Halbachsen gibt es Vorschriften [6.1]

     Bild 2106 Kopp-Ellipsenzirkel (Werkstatt J. Volmer, Chemnitz 1999)